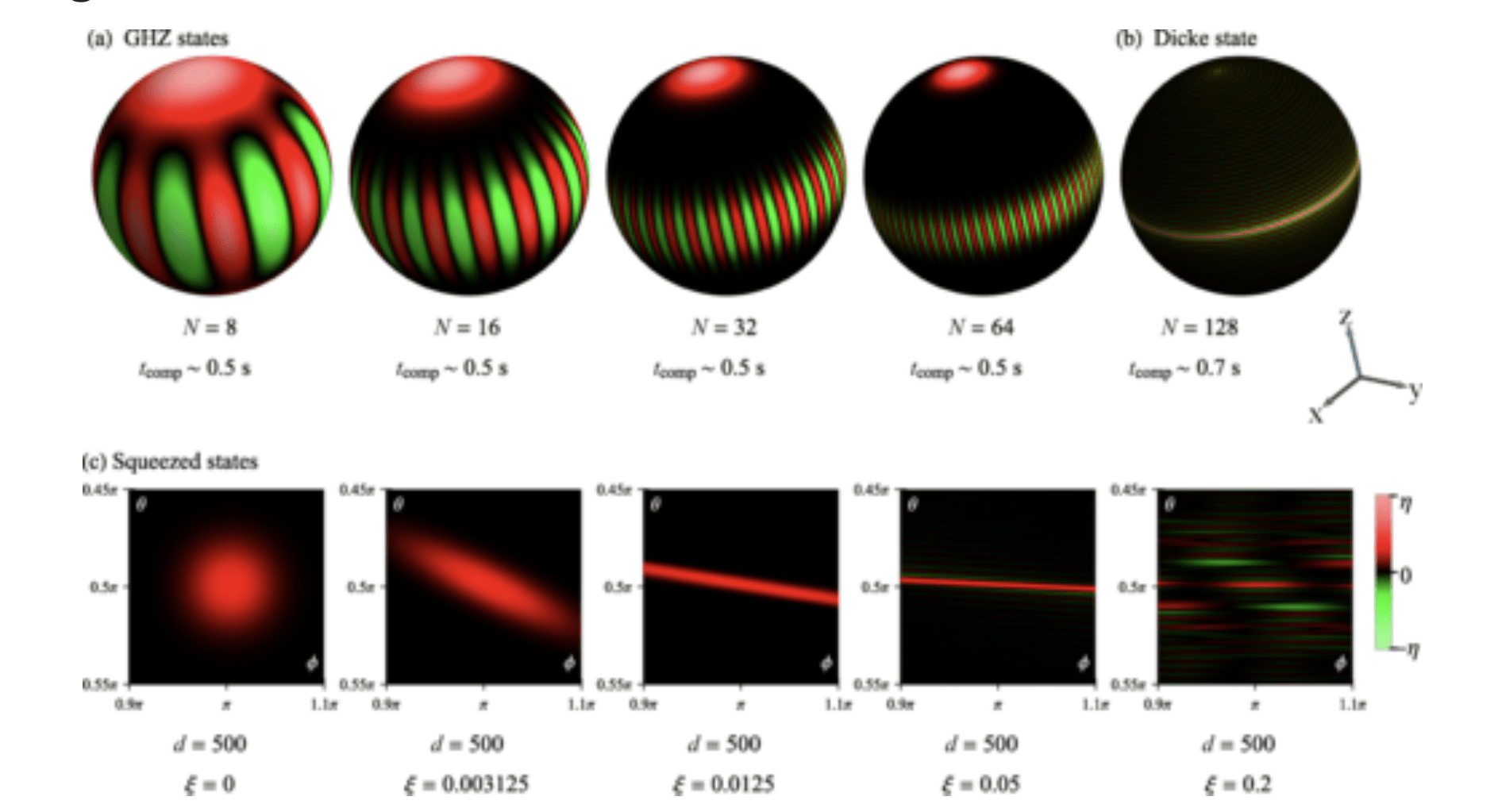
In December 2020, Bálint Koczor, Robert Zeier, and Steffen J. Glaser published their academic paper called Fast computation of spherical phase-space functions of quantum many-body states. The paper introduces new and faster ways to calculate these functions.
As quantum computers today have to be continuously updated and improved upon, so are the entangled quantum states they prepare getting more complex. This begs the question as to how would one study these quantum states as they gain many more dimensions. After all, the more dimensions there are, the harder it is to make studying them worthwhile and efficient.
One way to study these states is through phase spaces such as Wigner functions, as they provide a useful framework. The researchers focused on spherical phase spaces for finite-dimensional quantum states. These states were either of single qubits or the permutationally symmetric states of many connected qubits.
The methods in the paper are proven to be faster than traditional methods, as they are efficient in computing the corresponding spherical phase-space functions at least one order of magnitude faster.
Theorists and other researchers can study quantum many-body states in very large dimensions effectively using spherical phase-space techniques.