Quantum Algorithms Show Potential to Improve Numerical Integration Complexity

Quantum algorithms have shown superiority in various fields, but a general quantum algorithm for numerical integration, a crucial tool in complex science and engineering problems, is still missing. Classical integration algorithms face high computational complexity, while quantum algorithms exhibit acceleration superiority in some problems. However, a general quantum algorithm for numerical integrations is still absent. To address this, a general quantum integration algorithm (GQIA) is proposed that shows strong universality and operability. The algorithm achieves quantum encoding of any integrable functions through polynomial approximation, reducing computational complexity from ON to √ON. This work provides meaningful guidance for expanding the superiority of quantum computing.

What is the Current State of Quantum Algorithms for Numerical Integration?

Quantum algorithms have demonstrated their superiority in various application fields. However, a general quantum algorithm for numerical integration, a crucial tool for addressing complex science and engineering problems, is still lacking. Numerical integration is a classical and important problem with a wide range of applications in many fields such as physics, chemistry, biology, computer science, and finance. Existing classical integration algorithms face high computational complexity, where n represents the number of points used for integration calculation over the interval. Quantum algorithms, on the other hand, exhibit acceleration superiority over classical algorithms in some problems. For example, Shor’s integer factorization algorithm shows exponential acceleration over classical algorithms. Grover’s algorithm has quadratic acceleration over the classical algorithms in solving unordered database search problems. The HHL algorithm for solving systems of linear equations also exhibits exponential acceleration and is widely used in machine learning and other fields. Despite these advancements, a general quantum algorithm for numerical integrations is still absent.

How are Definite Integrations Approximated by Classical Numerical Methods?

Definite integrations are commonly approximated by classical numerical methods. For example, interpolation integration formulas include Newton-Cotes formula, Complex quadrature formula, Romberg formula, and Gauss formula. The algebraic accuracy of Newton-Cotes formula and Complex quadrature formula is n, where n is the number of interpolation nodes. But when n is greater than 7, these methods lose their effectiveness. The algebraic accuracy of Romberg formula is 2n and the algebraic accuracy of Gauss formula is 2n – 1. These interpolation integration formulas utilize the n order polynomials value at n interpolation points to approximate the integrations and their complexity is On. Besides that, the Monte Carlo integration (MCI) method generates n random numbers in the integration area S. The number of random numbers in the integration area is m, thus the integration is approximately equal to m/Sn. The complexity of MCI method is On, and error is O 1/n, which the error can be reduced by key sampling and Quasi-monte Carlo method etc. In all, the complexity of these classical algorithms is O n, that is high compared with quantum algorithms.

What Quantum Algorithms Have Been Proposed to Reduce the Complexity of Classical Algorithms?

To take advantage of quantum acceleration to reduce the complexity of classical algorithms, some quantum algorithms have been proposed. For example, Acioli et al. proposed a Quantum Monte Carlo (QMC) integration algorithm with quadratic acceleration for periodic functions. Abrams et al. proposed a fast quantum integration algorithm by using the Grover’s mean and quantum counting, which obtains exponential speed acceleration and quadratic acceleration in comparison with classical deterministic and probabilistic methods. However, the function is required to be discrete Boolean type in this method. Shimada et al. presented the quantum coin algorithm based on the quantum supersampling algorithm achieving quadratic acceleration, but the value of the functions is limited to 0-1. Heinrich raised a quantum integration algorithm with quadratic acceleration for Sobolev-like high-dimensional function. DeWitt-Morette et al. proved a quantum algorithm with exponential acceleration over deterministic classical algorithms on the functions of Holder class. Heinrich proposed a quantum integration algorithm on the Lebesgue space which proves the algorithm is optimal. Rebentrost et al. presented an optical quantum multidimensional integration algorithm which demonstrates quadratic acceleration over MC method. These algorithms mentioned above have limitations on the type of integration function.

What are the Limitations and Controversies of Existing Quantum Algorithms?

In addition to the limitations on the type of integration function, some quantum and classical hybrid integration algorithms have also been proposed. For example, Suzuki et al. raised a hybrid integration method to simplify the circuit depth. However, some are controversial over acceleration capability. For instance, the MCI method based on quantum amplitude estimation (QAE) can bring quadratic acceleration, but Kaneko et al. confirmed that the probability distribution of the initial state coding prepared by the Grover-Rudolph method does not reflect the quantum advantage. Existing classical integration algorithms face high computational complexity and quantum algorithms face low generality problems.

What is the Proposed Solution to These Problems?

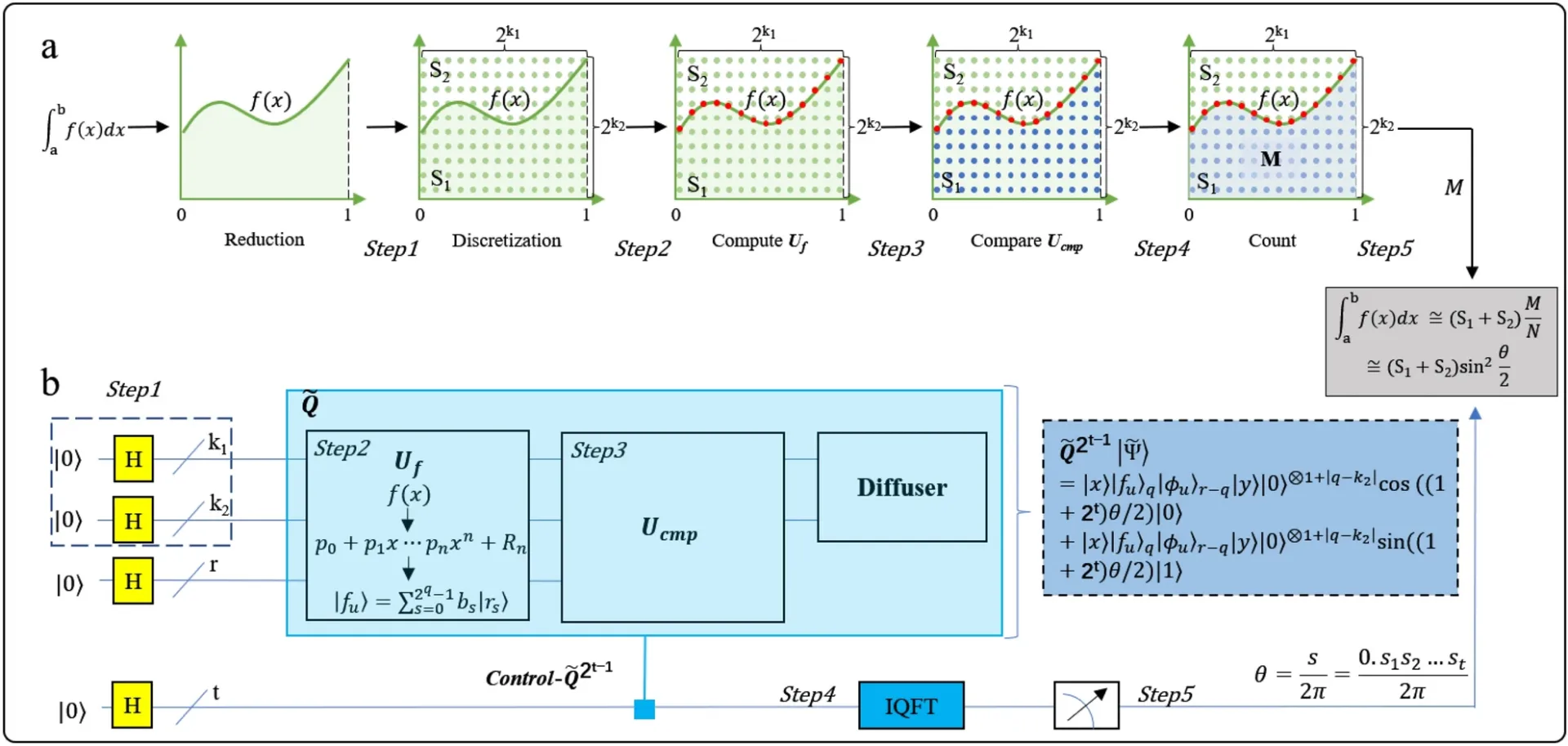
To address these issues, a general quantum integration algorithm (GQIA) is proposed that eliminates these shortages, showing strong universality and operability. The algorithm first proposes a quantum integration algorithm suitable for any continuous functions that can be approximated by polynomials. The algorithm achieves quantum encoding of any integrable functions through polynomial approximation, then constructs a quantum oracle to mark the number of points in the integration area, and finally converts the statistical results into the phase angle in the amplitude of the superposition state. The quantum algorithm introduced in this work exhibits quadratic acceleration over the classical integration algorithms by reducing computational complexity from ON to √ON. This work addresses the crucial impediments for improving the generality of quantum integration algorithm, which provides a meaningful guidance for expanding the superiority of quantum computing.