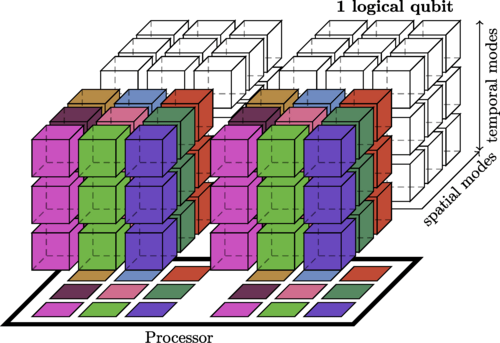
Élie Gouzien and Nicolas Sangouard of the French Alternative Energies and Atomic Energy Commission investigated the potentials of quantum memory in computations. From their research, they demonstrated that quantum computers with quantum memory installed can perform calculations with 3 orders of magnitude fewer qubits in their processor than standard architectures. They also outlined that installing quantum information storage will enable quantum computers to be built with fewer qubits in their processors.
Results of the research showed that using a 2D grid of qubits connected to a quantum memory that is organized in 3D was able to factor a 2048 bit RSA integer with just 13436 qubits. This is very far from over 20 million qubits that would have been required for the same task when using the standard superconductor qubit technologies which is one of the most promising technologies.
However, the standard superconductor qubit technology can perform factorization in 8 hours while the quantum memory architecture will use 177 days which is very far from ideal.

Conclusively, when a quantum computer using a small processor and a quantum information storage unit is used for factorization, there is a large and significant reduction in the magnitude of the number of qubits required to completely process the task. This is not the same for standard architectures which use up to 20 million qubits. Also, a barrier was encountered on the time it took to complete factorization as it was observed that the quantum architecture took a long time up to 177 days against 8 hours used by the standard architecture.
Élie Gouzien and Nicolas Sangouard recommended further investigation to be conducted on the quantum architecture, as a smaller magnitude of qubit will be much more useful for the long term. This investigation will be to devise means to reduce the time required for the quantum architecture to complete factorization.
Read the original paper here “Factoring 2048-bit RSA Integers in 177 Days with 13 436 Qubits and a Multimode Memory”.