Quantum-Inspired Algorithm Challenges Gaussian Boson Sampling’s Edge in Graph-Theoretical Problems

Researchers from the University of Chicago, Korea Advanced Institute of Science and Technology, and École Polytechnique de Montréal have developed a quantum-inspired classical algorithm for graph-theoretical problems. The algorithm, based on Gaussian boson sampling principles, was compared to other samplers and found to have no significant advantage. However, the research is significant as it presents a new approach to solving graph-theoretical problems and raises questions about the quantum advantage of Gaussian boson samplers. The algorithm could have practical applications in fields such as data mining and bioinformatics, and could lead to more practical uses of quantum devices.

What is the Quantum-Inspired Classical Algorithm for Graph Problems?

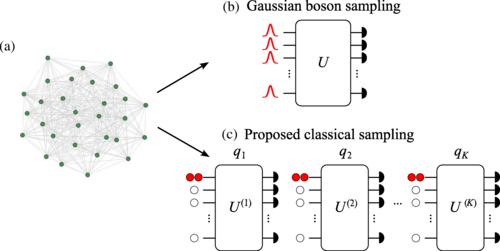
A team of researchers from the Pritzker School of Molecular Engineering at the University of Chicago, the Department of Physics at the Korea Advanced Institute of Science and Technology, the Department of Computer Science at the University of Chicago, and the Department of Engineering Physics at École Polytechnique de Montréal have developed a quantum-inspired classical algorithm that can be used for graph-theoretical problems. These problems include finding the densest k-subgraph and finding the maximum weight clique. The algorithm is based on the principles of Gaussian boson sampling.

The researchers observed that the adjacency matrix of a graph, which is encoded in a Gaussian boson sampler, is always nonnegative. This observation is crucial because computing the output probability of Gaussian boson sampling restricted to a nonnegative adjacency matrix is thought to be easier than general cases. The team then programmed a given graph problem into their efficient classical algorithm.

How Does the Algorithm Compare to Other Samplers?

The researchers compared the performance of their quantum-inspired classical sampler with ideal and lossy Gaussian boson samplers and a uniform sampler. They used these samplers to find the densest k-subgraph and the maximum weight clique. The results showed that the advantage from Gaussian boson samplers is not significant in general.

However, the team also discussed the potential advantage of a Gaussian boson sampler over the proposed quantum-inspired classical sampler. They noted that while the graph-theoretical problems they considered have been considered applications of Gaussian boson sampling, it has been a longstanding open question whether they provide a provable quantum computational advantage.

What is the Significance of this Research?

This research is significant because it presents a new approach to solving graph-theoretical problems. The quantum-inspired classical algorithm developed by the researchers has the same property as a Gaussian boson sampler in that the sampler more frequently samples subgraphs with many perfect matchings, implying a high density. This property is crucial for solving such problems.

The research also raises questions about the quantum advantage of the Gaussian boson sampler for solving graph problems. The team’s proposal suggests that the quantum advantage of the Gaussian boson sampler may not be as significant as previously thought.

What are the Practical Applications of this Research?

The graph-theoretical problems that the researchers focused on, such as finding the densest k-subgraph and finding the maximum weight clique, have potential applications in a wide range of fields. These include data mining and bioinformatics.

The researchers’ work opens up the possibility of taking advantage of quantum computational advantage from noisy intermediate-scale quantum (NISQ) devices to solve practical problems. This is an important step beyond proof-of-principle experiments and could lead to more practical applications of quantum devices.

What are the Future Directions for this Research?

The researchers’ work highlights the need for further scrutiny of the problems’ complexity and potential ways of simulating the quantum algorithm using a classical counterpart. This is crucial for claiming and exploiting the potential quantum advantage more rigorously.

The team’s research also suggests that potential applications of quantum devices sometimes turn out to be classically simulable. This observation could have implications for future research and development in the field of quantum computing.