Adiabatic Gauge Potential: Revolutionizing Quantum Calculations and Unveiling Future Applications

The Adiabatic Gauge Potential (AGP) is a fundamental concept in quantum physics, used to formalize the concept of adiabatic transport. It can be represented numerically as a tensor network, allowing for efficient numerical optimization. The AGP can improve the reliability and efficiency of quantum calculations, particularly those involving low-energy excited states. It has numerous practical applications, including optimal control in counter-diabatic driving, adiabatic quantum computation, and studying quantum chaos of many-body systems. The future of AGP in quantum physics is likely to involve further exploration of its potential applications and improvements to its numerical optimization methods.

What is the Adiabatic Gauge Potential and How is it Used in Quantum Physics?

The adiabatic gauge potential (AGP) is a fundamental concept in quantum physics. It is the generator of adiabatic transformations, which are slow, continuous changes in a quantum system. The AGP is used to formalize the concept of adiabatic transport, which is a key principle in quantum physics. The adiabatic theorem states that a quantum system that starts in an eigenstate of a Hamiltonian will remain in that eigenstate as long as the Hamiltonian changes slowly enough. This principle has numerous applications in quantum state preparation, quantum computation, and thermodynamics.

The AGP can be represented numerically as a tensor network, specifically a matrix product operator (MPO). This representation allows for efficient and reliable numerical optimization of the AGP. This optimization method provides a general way of performing adiabatic evolution of a matrix product state (MPS), with potential extensions to other tensor networks. This is a significant advancement over previous methods of adiabatic evolution, which were based on parent Hamiltonian constructions.

How Can the Adiabatic Gauge Potential Improve Quantum Calculations?

The AGP can be used to improve the reliability and efficiency of quantum calculations, particularly those involving low-energy excited states. These states provide important physical information about a quantum system, such as information on quantum phase transitions and critical points. However, calculating these states can be computationally challenging, especially near critical points where the spectrum is dense.

By using the AGP to adiabatically evolve MPS excitations from far from the critical point towards it, calculations can be made more reliable, accurate, and efficient. This method is more effective at finding a set of low-energy eigenstates at the critical point than standard excited-state density-matrix renormalization group (DMRG) methods. This is a significant advancement in the field of quantum physics, as it allows for more accurate and efficient calculations of important physical properties of quantum systems.

What are the Practical Applications of the Adiabatic Gauge Potential?

The AGP has numerous practical applications in the field of quantum physics. It can be used for optimal control in counter-diabatic driving, in adiabatic quantum computation, and in studying the quantum chaos of many-body systems. It can also be used to automatically scan the entire phase diagram of a quantum system, which is a key task in understanding the behavior of the system.

The AGP can also be used to improve tensor network optimization. By efficiently transporting eigenstates to quantum criticality and performing intermediary DMRG optimizations along the way, ground and low-lying excited states can be computed faster and more reliably. This method also allows for the detection of the critical point based on the norm of the AGP, which is a significant advancement in the field.

How Does the Adiabatic Gauge Potential Work in Practice?

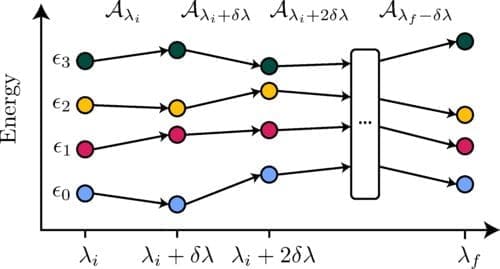
In practice, the AGP is used to adiabatically evolve energy eigenstates. The process begins with the lowest-lying states at a certain parameter point. The AGP is then computed at this point to propagate these states to the next parameter point. This process is repeated iteratively until the final parameter point is reached.

The spacing between parameter points can be automatically adjusted based on the norm of the AGP. This allows for more steps to be added where necessary, such as near quantum critical points. Optimization algorithms like the DMRG can be used to find more accurate states during the course of the adiabatic evolution.

What is the Future of the Adiabatic Gauge Potential in Quantum Physics?

The AGP has the potential to significantly advance the field of quantum physics. Its ability to improve the reliability and efficiency of quantum calculations, particularly those involving low-energy excited states, is a significant advancement. Its numerous practical applications, from optimal control in counter-diabatic driving to automatic scanning of phase diagrams, make it a valuable tool in the field.

The future of the AGP in quantum physics is likely to involve further exploration of its potential applications and improvements to its numerical optimization methods. As our understanding of the AGP and its applications continues to grow, it is likely to become an increasingly important tool in the field of quantum physics.