Quantum Master Equations: Key to Modeling Microscopic Systems

Researchers from RMIT University in Melbourne, Australia, and the Università degli Studi di Padova in Italy have created a tutorial on quantum master equations. These equations are vital for modelling the dynamics of microscopic systems in fields such as quantum optics and quantum information processing. The tutorial covers key methods such as the Lindblad master equation, Redfield relaxation, and Floquet theory, and provides practical examples of implementation using Python. It also discusses future challenges and directions in the field, including computational requirements and the extension of methods to more complex systems.

What are Quantum Master Equations and Why are They Important?

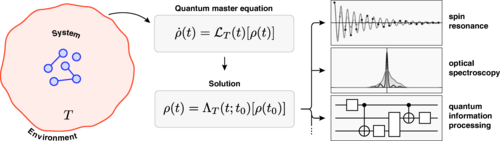
Quantum master equations are a crucial tool in modeling the dynamics of a variety of microscopic systems. These systems range from quantum optics and quantum information processing to energy and charge transport, electronic and nuclear spin resonance, photochemistry, and more. The equations are used to describe the probabilistic combination of states in these systems, which can be complex and intricate.

The tutorial by Francesco Campaioli, Jared H Cole, and Harini Hapuarachchi, researchers from the School of Science at RMIT University in Melbourne, Australia, and the Dipartimento di Fisica e Astronomia G Galilei and Padua Quantum Technologies Research Center at Università degli Studi di Padova in Italy, provides a concise and pedagogical introduction to quantum master equations. The tutorial is designed to be accessible to a broad cross-disciplinary audience, guiding readers through the basics of quantum dynamics with hands-on examples that increase in complexity.

The tutorial covers essential methods such as the use of the Lindblad master equation, Redfield relaxation, and Floquet theory. It also introduces techniques such as the Suzuki-Trotter expansion and numerical approaches for sparse solvers. These methods are illustrated with code snippets implemented in Python and other languages, which can be used as a starting point for generalization and more sophisticated implementations.

How are Quantum Master Equations Used in Quantum Optics and Quantum Computing?

In quantum optics and quantum computing, quantum master equations are used to model the dynamics of systems that can be described as a probabilistic combination of states. For example, the concentration dynamics of a chemical reaction, where some reactants lead to some products, can be described by differential equations. These equations can be easily solved to obtain the transient and steady-state concentrations of the reactants and products as a function of their initial concentrations and transition rates.

In quantum systems, however, we must take into account that coherent superpositions of states participate in the evolution as prescribed by Schrödinger’s equation. This means that a vector of probabilities is no longer sufficient to completely describe the dynamics of the system, as different phases will lead to different solutions. Master equations for these systems are therefore more complex and require a deeper understanding of quantum dynamics.

What are the Key Techniques and Methods in Quantum Master Equations?

The tutorial covers several key techniques and methods in quantum master equations. One of these is the Lindblad master equation, which is used to describe the dynamics of open quantum systems. The Lindblad equation is a type of master equation that includes a term to account for the effects of the environment on the quantum system.

Another important method covered in the tutorial is Redfield relaxation, which is used to describe the relaxation processes in quantum systems. This method is particularly useful in quantum optics and quantum information processing, where relaxation processes play a crucial role.

The tutorial also introduces Floquet theory, which is used to analyze the behavior of periodically driven systems. This theory is particularly useful in quantum computing, where quantum systems are often driven by periodic external fields.

How are Quantum Master Equations Implemented in Practice?

The tutorial provides practical examples of how to implement quantum master equations using Python and other programming languages. These examples include code snippets that can be used as a starting point for more general and sophisticated implementations.

One of the techniques illustrated in the tutorial is the Suzuki-Trotter expansion, which is a method for approximating the solution of a differential equation. This technique is particularly useful in quantum computing, where it is often used to simulate the evolution of quantum systems.

The tutorial also introduces numerical approaches for sparse solvers, which are algorithms for solving systems of linear equations where the coefficient matrix is sparse. These methods are particularly useful in quantum optics and quantum information processing, where the systems of interest often have a large number of states but only a small number of transitions between them.

What are the Future Directions and Challenges in Quantum Master Equations?

The tutorial concludes with a discussion of future directions and challenges in quantum master equations. One of the key challenges is the computational requirements for solving these equations, particularly for large systems. The tutorial discusses methods for reducing the memory and operations requirements, such as the use of sparse solvers and other numerical methods.

Another challenge is the extension of these methods to more complex systems and processes. For example, the tutorial discusses the extension of Floquet theory to decoherence processes, which are processes that cause a quantum system to lose its quantum coherence.

The tutorial also highlights the importance of understanding the physical implications of the mathematical formalism of quantum master equations. This includes understanding the physical meaning of the Lindblad form of the master equation, the conditions under which the Redfield approximation is valid, and the physical interpretation of the Floquet modes and quasi-energies.